標準偏差:データのばらつきを理解する

AIの初心者
先生、「標準偏差」ってどういう意味ですか?AIの勉強で出てきたんですが、よく分からなくて…

AI専門家
なるほど。標準偏差は、データが平均値からどれくらいばらついているかを表す値だよ。例えば、クラスのテストの点数を考えてみよう。平均点が同じでも、みんなが同じような点数か、高い点と低い点が混ざっているかで、データのばらつき具合は違うよね。

AIの初心者
なんとなくイメージはわきます。ばらつき具合ですね。でも、AIとどう関係があるんですか?

AI専門家
AIでは、データを分析して学習することが多いんだけど、そのデータのばらつき具合を理解することはとても重要なんだ。例えば、AIに画像を分類させたいとき、データのばらつきが大きいと、AIはうまく分類できない可能性がある。標準偏差はそのばらつき具合を数値で表してくれるから、AIの精度を上げるのに役立つんだよ。
標準偏差とは。
人工知能の分野でよく使われる「標準偏差」という用語について説明します。標準偏差とは、数学や統計学、機械学習といった分野で、データのばらつき具合を示す指標です。
標準偏差とは

標準偏差とは、数値データのばらつき具合、つまり散らばり具合を表す指標です。平均値だけではデータの全体像を掴むことができません。例えば、ある学校の算数のテストで、A組とB組の平均点がどちらも70点だったとします。しかし、A組は全員が70点付近の点数を取っていたのに対し、B組は30点の人もいれば100点の人もいるなど、点数のばらつきが大きかったとしましょう。このような場合、平均点は同じでも、二つの組のテスト結果には大きな違いがあります。標準偏差は、まさにこの違いを数値化してくれるのです。
標準偏差は、個々のデータが平均値からどれくらい離れているかを平均的に示しています。計算方法は、まず各データと平均値の差を二乗します。これは、平均値からの離れ具合を強調するためです。次に、それらの二乗した値の平均を求めます。最後に、その値の平方根を計算することで標準偏差が得られます。平方根をとる理由は、二乗した値を元のスケールに戻すためです。
標準偏差が小さいということは、データが平均値の近くに集まっていることを意味します。例えば、工場で生産されるネジの長さを測った結果、標準偏差が小さければ、どのネジもほぼ同じ長さで生産されていると判断できます。これは、製品の品質が安定していることを示しています。逆に、標準偏差が大きい場合は、データが平均値から大きく散らばっていることを意味します。先ほどのネジの例で言えば、標準偏差が大きい場合は、ネジの長さにばらつきがあり、品質が安定していない可能性があります。
このように、標準偏差はデータのばらつき具合を数値化することで、データの性質をより深く理解するのに役立ちます。この指標は、品質管理や金融、医療など、様々な分野で活用されています。例えば、金融では投資のリスクを評価する際に、医療では検査データの分析などに用いられています。
| 標準偏差とは | 数値データのばらつき具合を表す指標 |
|---|---|
| 計算方法 | 1. 各データと平均値の差を二乗 2. 二乗値の平均を計算 3. 平均値の平方根を計算 |
| 標準偏差が小さい場合 | データが平均値付近に集中、品質が安定 |
| 標準偏差が大きい場合 | データが平均値から分散、品質が不安定 |
| 活用分野 | 品質管理、金融、医療など |
計算方法

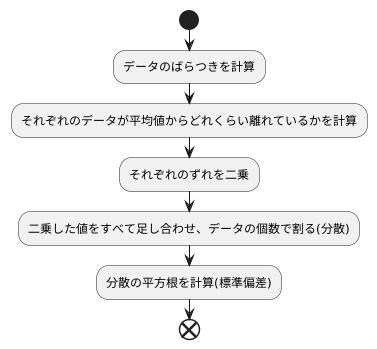
計算方法は、少し込み入った手順を踏みますが、一つずつ丁寧に見ていくことで理解を深めることができます。標準偏差とは、データのばらつき具合を示す指標です。このばらつき具合を測るために、いくつかの段階を踏みます。まず、それぞれのデータが平均値からどれくらい離れているかを計算します。平均値は、全体のデータの平均です。それぞれのデータから平均値を引くことで、個々のデータの平均からのずれが分かります。このずれは、プラスやマイナスの値になります。次に、一つ前の段階で計算したそれぞれのずれを二乗します。二乗とは、同じ数を二回かけることです。例えば、3かける3は9です。マイナスの数を二乗するとプラスの値になります。二乗する理由は、平均値からのずれの大きさを重視するためです。ずれがプラスかマイナスかは関係なく、ずれの大きさを重視するために二乗を行います。また、平均値から大きく離れた値の影響をより強く反映させる効果もあります。次に、二乗した値をすべて足し合わせ、データの個数で割ります。これは、二乗したずれの平均を求めていることになります。この値を「分散」と言います。分散は、データのばらつき具合を表す指標の一つですが、二乗しているため元のデータと単位が異なってしまいます。そこで、最後に分散の平方根を計算します。平方根とは、二乗してその数になる値のことです。例えば、9の平方根は3です。平方根を計算することで、元のデータと同じ単位に戻すことができます。こうして求められた値が標準偏差です。標準偏差は、データのばらつき具合を直感的に理解しやすい指標として使われます。計算式は複雑に見えるかもしれませんが、計算機などを利用すれば簡単に計算できますので、安心してください。
分散との関係

データのばらつき具合を測る尺度として、分散と標準偏差は切っても切れない関係にあります。分散とは、データが平均値からどれほど離れているかを平均的に示す値です。計算方法は、まず各データと平均値との差を求め、それを二乗します。次に、それらの二乗した値をすべて足し合わせ、データの個数で割ります。この計算により、データのばらつきの大きさが数値化されます。
しかし、分散には一つ欠点があります。それは、計算の過程でデータを二乗するため、元のデータとは単位が変わってしまうことです。例えば、身長のデータがセンチメートル単位で測られている場合、分散の単位は平方センチメートルとなってしまいます。平方センチメートルは面積の単位であり、身長のばらつきを表すには直感的ではありません。
そこで登場するのが標準偏差です。標準偏差は、分散の平方根をとることで、元のデータと同じ単位に戻した値です。先ほどの身長の例でいえば、標準偏差の単位はセンチメートルとなり、身長のばらつきをより分かりやすく示すことができます。標準偏差は、平均値からどれくらいデータがばらついているかを、元のデータと同じ尺度で測ることができるため、データのばらつきを直感的に理解するのに役立ちます。
このように、分散と標準偏差は表裏一体の関係にあります。分散はばらつきの大きさを計算する基礎となり、標準偏差はその値をより解釈しやすい形に変換したものです。どちらの値も、データの分布を理解する上で重要な役割を果たします。特に、標準偏差はデータ分析の様々な場面で活用され、データの特性を把握するための重要な手がかりとなります。
| 尺度 | 定義 | 単位 | 利点 | 欠点 |
|---|---|---|---|---|
| 分散 | データが平均値からどれほど離れているかを平均的に示す値。各データと平均値の差を二乗し、その合計をデータの個数で割る。 | 元のデータの単位の二乗 | ばらつきの大きさを数値化 | 元のデータと単位が異なり、直感的でない |
| 標準偏差 | 分散の平方根。 | 元のデータと同じ単位 | 元のデータと同じ単位でばらつきを測れるため、直感的。 | – |
活用事例

標準偏差は、数値データのばらつき具合を測るものさしであり、様々な分野で活用されています。ものづくり、お金のこと、医療など、幅広い分野で重要な役割を担っています。ものづくりでは、製品の品質を保つために欠かせないものとなっています。例えば、工場で作られる部品の大きさや重さを測ると、どうしてもばらつきが生じます。このばらつきが大きすぎると、製品の性能に影響が出たり、不良品が増えたりする可能性があります。標準偏差を使うことで、このばらつき具合を数値で捉えることができます。ばらつきが大きすぎる場合は、製造工程を見直すことで、品質の向上に繋げることができます。
お金を扱う分野でも、標準偏差は重要な役割を担っています。例えば、株式投資では、株価の上がり下がりの大きさを標準偏差で表すことができます。標準偏差が大きいほど、株価の変動が激しく、投資のリスクが高いと言えます。逆に、標準偏差が小さいほど、株価は安定しており、投資のリスクは低いと言えます。投資家は、標準偏差を参考にしながら、自分のリスク許容度に応じた投資判断を行うことができます。
医療の分野でも、標準偏差は活用されています。健康診断などで血液検査を受けた際、検査結果には基準値が示されています。この基準値は、健康な人のデータをもとに算出された平均値から、標準偏差を使って一定の範囲を設定したものです。検査結果が基準値から大きく外れている場合、標準偏差を使ってそのずれの大きさを評価します。ずれが大きいほど、病気の可能性が高いため、精密検査が必要となる場合があります。このように、標準偏差は病気の早期発見にも役立っています。
このように、標準偏差は様々な分野で、データのばらつきを把握し、分析する上で欠かせないツールとなっています。標準偏差を理解し、活用することで、より的確な判断を行うことができます。
| 分野 | 活用例 | 標準偏差の役割 |
|---|---|---|
| ものづくり | 製品の大きさや重さ | ばらつきを数値化し、品質管理に役立てる |
| 金融 | 株価の変動 | 投資リスクの評価指標 |
| 医療 | 血液検査の基準値 | 病気の早期発見 |
正規分布との関係

標準偏差は、データのばらつき具合を示す統計的な指標であり、平均値からどれくらいデータが離れているかを表すものです。特に、釣鐘型の曲線で表される正規分布と組み合わせて用いることで、データの分布に関するより深い理解を得ることができます。正規分布は、自然界の様々な現象、例えば身長や体重の分布など、多くの場面で見られる分布です。この分布は、平均値を中心として左右対称であり、平均値付近にデータが集中し、平均値から離れるほどデータの数が少なくなるという特徴を持っています。
正規分布において、標準偏差は分布の広がり具合を表す重要な役割を果たします。具体的には、平均値から標準偏差1つ分の範囲内には、全体の約68%のデータが含まれます。平均値から標準偏差2つ分の範囲内には、全体の約95%のデータが含まれ、平均値から標準偏差3つ分の範囲内には、全体の約99.7%のデータが含まれます。つまり、ほぼ全てのデータが平均値から標準偏差3つ分の範囲内に収まるということです。
この標準偏差と正規分布の性質を利用することで、ある特定の範囲にデータがどれくらいの確率で含まれるのかを推定することができます。例えば、ある工場で生産される部品の重さが正規分布に従っているとします。この時、標準偏差を計算することで、ある一定の重さの範囲内にどれだけの割合の部品が含まれるのかを予測することが可能になります。これは、製品の品質管理を行う上で非常に有用な情報となります。例えば、製品の重さが規格の範囲外になる確率を計算することで、不良品の発生率を予測し、生産工程の改善に役立てることができます。また、顧客からの注文に対して、納期通りに製品を供給できるかどうかの予測にも役立ちます。このように、標準偏差と正規分布は、様々な場面でデータ分析に活用され、意思決定を支援するための重要なツールとなっています。
| 標準偏差 | データのばらつき具合を示す統計的指標 |
|---|---|
| 正規分布 | 釣鐘型の曲線で表される分布 自然界の様々な現象で見られる 平均値を中心として左右対称 平均値付近にデータが集中 平均値から離れるほどデータが少ない |
| 標準偏差と正規分布の関係 | 標準偏差は正規分布の広がり具合を表す 平均値 ± 標準偏差1つ分: 約68%のデータが含まれる 平均値 ± 標準偏差2つ分: 約95%のデータが含まれる 平均値 ± 標準偏差3つ分: 約99.7%のデータが含まれる |
| 活用例 | 品質管理 不良品発生率の予測 納期予測 |
まとめ

たくさんの数値を扱うとき、その数値たちがどのくらい散らばっているかを知ることはとても大切です。例えば、テストの点数を考えてみましょう。平均点が同じでも、全員の点数が平均点付近に集まっている場合と、高い点数の人と低い点数の人が混ざっている場合では、そのテストの様子は全く違います。このような数値の散らばり具合を表すのが標準偏差です。
標準偏差を計算するのは少し手間がかかります。まず、それぞれの数値が平均値からどれくらい離れているかを計算し、その値を二乗します。次に、二乗した値をすべて足し合わせ、数値の個数で割ります。これが分散と呼ばれる値です。そして、分散の平方根をとると、標準偏差が求まります。計算は複雑ですが、最近は表計算ソフトなどを使えば簡単に計算できますので、安心してください。
標準偏差は、分散と密接な関係があります。分散は、データの散らばり具合を数値で表したものですが、単位が元のデータの二乗になってしまうため、解釈しづらいことがあります。そこで、分散の平方根をとることで、元のデータと同じ単位で散らばり具合を表すことができるのです。これが標準偏差です。
標準偏差は、様々な分野で活用されています。例えば、工場で製品の品質をチェックする場合、不良品の発生率を減らすために、製品の寸法などのばらつきを標準偏差を用いて管理します。また、金融の分野では、投資のリスクを評価するために標準偏差が使われます。医療の分野では、患者の検査データのばらつきを分析するために標準偏差が用いられることもあります。このように、標準偏差は、データの性質を理解し、より良い判断をするために欠かせない道具となっています。
特に、標準偏差は正規分布と組み合わせることで、より強力な分析ツールとなります。正規分布とは、平均値を中心とした左右対称の釣鐘型の分布のことです。標準偏差を用いることで、データが正規分布に従っている場合、平均値からどのくらいの範囲にどのくらいの割合のデータが含まれているかを推定することができます。これにより、将来の予測や分析の正確さを高めることができます。標準偏差を理解し、活用することで、データ分析の質を格段に向上させることができるでしょう。
| 用語 | 説明 | 関連する用語 | 活用例 |
|---|---|---|---|
| 標準偏差 | 数値の散らばり具合を表す指標。分散の平方根。 | 分散、正規分布 | 品質管理、リスク評価、検査データ分析 |
| 分散 | データの散らばり具合を表す指標。単位が元のデータの二乗になるため解釈しづらい。 | 標準偏差 | |
| 正規分布 | 平均値を中心とした左右対称の釣鐘型の分布。標準偏差と組み合わせることで強力な分析ツールとなる。 | 標準偏差 | 将来予測、分析の正確性向上 |
